RSASSA-PSS algorithms – Digital Signatures
9.4.2 RSASSA-PSS algorithms
The TLS 1.3 SignatureScheme data structure defines two types of RSASSA-PSS algorithms: algorithms with public key OID rsaEncryption and algorithms with public key OID RSASSA-PSS.
An Object Identifier (OID) is a unique number standardized by the International Telecommunication Union (ITU) and ISO/IEC to globally and unambiguously identify an object, attribute, or concept.
The OID rsaEncryption identifies a specific representation of the RSA public and private keys [94]. The public key is represented by the RSA modulus n and the RSA public exponent e. The private key is represented by a set of values that includes the RSA modulus n, the RSA public exponent e, the RSA private exponent d, the secret primes p and q, the exponents d (mod p − 1) and d (mod q − 1), and the coefficient q−1 (mod p).
OID RSASSA-PSS identifies the RSASSA-PSS encryption scheme.AlgorithmIdentifier field associated with OID RSASSA-PSS specifies the hash function, the mask generation algorithm, and the length of the salt. Supported hash functions are SHA-256, SHA-384, and SHA-512, where the number indicates the length of the hash value in bits. The digest used in the mask generation function corresponds to the hash function used for signing, while the length of the salt is equal to the length of the hash value.
RSASSA-PSS algorithms combine the RSASP1 and RSAVP1 functions with an encoding method called EMSA-PSS, and the mask generation function 1 defined in RFC 8017.
The EMSA-PSS encoding is configured by selecting a hash function, a mask generation scheme, and the length of a salt. A message M is encoded using EMSA-PSS as follows:
- Compute the hash value H = h(M).
- Generate a random salt s.
- Concatenate the previously computed values to:
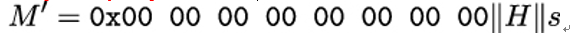
- With the result from the previous step, compute the hash value H′ = h(M′).
- Generate a 0x00-byte string P of a suitable length defined in RFC 8017, and compute D = P∥0x01∥s.
- Compute the mask μ = MGF(H′,l), where MGF is the chosen mask generation function and l is the number of bytes determined by the values computed in the previous steps.
- Compute the masked value Dm as Dm = D ⊕ μ. Here, the operator ⊕ denotes exclusive OR.
- Output M′ = Dm∥H′∥0xbc.
To generate the signature for message M with her private RSA key (n,d), Alice performs the following steps:
- Compute the EMSA-PSS encoding of the plaintext message M:
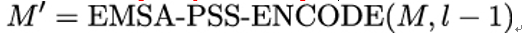
with l being the length of the RSA modulus n.
2. Convert the encoded message M′ to its integer representation as
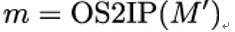
3. Compute the integer representation of the signature:
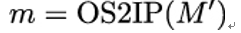
4. Convert s to a byte string of length k as:
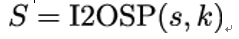
- Output the signature S.
After receiving the message M and the accompanying signature S from Alice, Bob uses Alice’s public key (n,e) to verify the signature as follows:
- Convert signature S into its integer representation as:
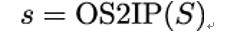
2. Compute the integer representation of message M using the RSAVP1 function and Alice’s public RSA key (n,e):
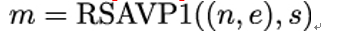
3. Convert m into the encoded message M′:
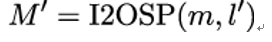
where l′ is the byte length n − 1.
4. Compute the EMSA-PSS verification function on message M and the encoded message M′ to determine whether they are equal:

In contrast to other RSA-based signature schemes defined in RFC 8017, RSASSA-PSS is probabilistic rather than deterministic because it incorporates a randomly generated salt. The salt increases the security of the signature scheme by enabling a more conservative security proof than deterministic alternatives.