General considerations – Digital Signatures
9.1 General considerations
Assume Alice has generated herself a key pair (PKAlice,SKAlice) within some asymmetric cryptosystem. If Alice uses her private key SKAlice to compute some output s = sigAlice(x) based on an input x, this is an operation that can, at least in principle, only be performed by Alice because she is the only one to know SKAlice. This is fundamentally different from the situation when symmetric cryptosystems are used because here, at least two parties know the key K and can perform the same operations.
The fact that only Alice can compute s for some given input x motivates us to interpret sigAlice as a digital signature. However, for this to work in practice, some important points need to be clarified:
- There must be some way to verify that Alice has produced the signature and that the signed document has not been changed since it has been signed. As this should be possible for any party, the verification step should not involve any secret information, but must be based on the public key PKAlice.
- It must not be possible for an attacker to deduce SKAlice from the signature value s, or to compute s by some other means without knowing SKAlice.
- As with physical, handwritten signatures, the length of the digital signature should be independent from the length of a signed document m. This can be achieved by applying SKAlice on a fixed-length hash value x = H(m) instead of m itself.
- As we have seen in Chapter 7, Public-Key Cryptography, operations involving the private key are costly. This is another reason for working with (cryptographic) hash values, which will be shorter than the original documents in most cases.
The use of cryptographic hash functions in connection with digital signatures typically requires at least one important security property of the hash function H, namely collision resistance. This means that it must be hard for attacker Eve to find two different inputs x1,x2 with the same hash value H(x1) = H(x2).
If Eve cannot construct arbitrary collisions, she is also unable to construct a specific collision where she is given some message m, and has to find another input message m so that H(m) = H(m). This weaker form of collision resistance is also called second preimage resistance and is of special importance for digital signatures: if Eve manages to find a second preimage m, we have
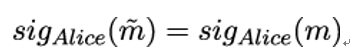
and Eve could replace m with m.
We will discuss collision resistance in greater detail in Chapter 11, Hash Functions and Message Authentication Codes. For now, we will simply assume that H is a secure cryptographic hash function, which means H is a hash function that has this property.
Based on this assumption, digital signatures can be used as tools for message authentication and entity authentication (see Chapter 15, Authenticated Encryption). But because no one but Alice can have produced the signature s over m, Alice cannot repudiate afterward having signed m, or having sent a message involving the signature. This property constitutes a new security objective called non-repudiation. Digital signatures are the only cryptographic mechanism by which non-repudiation can be achieved.
In the next two sections, we will see how, in principle, digital signatures can be realized based on the asymmetric cryptosystems we learned about in the previous two chapters. As they are based on the same mathematical problems (factorization problem or discrete logarithm problem), digital signatures basically inherit the same security properties as the corresponding asymmetric cryptosystems. Note however that in order to fully specify a real-world digital signature scheme, many more details need to be fixed, such as how to encode and pad the message, how to generate and use nonces, and so on. You can find some of these nuts and bolts later in this chapter in Section 9.4, Digital signatures in TLS.