IT Certification Exams and Digital Signatures

Elliptic Curve Digital Signature Algorithm (ECDSA) – Digital Signatures

• Ella Andrus
• 2022-07-152024-08-31
• 0

9.3.2 Elliptic Curve Digital Signature Algorithm (ECDSA)

When transferring the DSA algorithm to an elliptic curve E, we just switch the group from 𝔽p∗ to E, so the basic steps will stay the same. We just have to ensure that we switch the objects correctly:

• In DSA, p − 1 signifies the group order of 𝔾 = 𝔽p∗ and q signifies the order of the cyclic subgroup generated by g ∈𝔾. In ECDSA, the group order of E is N, where N is the number of points on E, and n is the order of the cyclic subgroup generated by the multiples of G ∈ E.N can be estimated by using Hasse’s theorem (see Chapter 8, Elliptic Curves), and n is automatically a divisor of N, because it is the order of a subgroup of E.
• Numbers, if they signify how often a group operation is applied, remain being numbers in the ECDSA. On the other hand, a number A, when seen as an element of 𝔽p∗, becomes a point P on E. In particular, this means that Alice’s private key α is still a number in ECDSA, whereas her public key PKAlice becomes a point on E.
• The group operation is written additively in E, so powers gx become products xG on E, and products x ⋅ y become sums P + Q on E.

Bearing this in mind, formulating the ECDSA is not very difficult:

To set up the scheme, Alice and Bob agree on:

• An elliptic curve E of order N over some finite field 𝔽
• A point G ∈ E, which generates a large cyclic subgroup of order n

To generate her signing key, Alice performs the following steps:

1. She takes a random α, where 0 < α < n, as her secret signing key SKAlice.
2. Her public key PKAlice is the point A = α ⋅ G ∈ E.

To sign a message m, Alice takes the following steps:

1. She applies a hash function H to m. The result H(m) should be in the range 0 < H(m) < n.
2. She picks a random integer k, where 0 < k < n, computes the point P = k ⋅ G = (xP ,yP ) on E, and sets

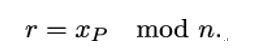
3. Finally, Alice finds an integer s such that

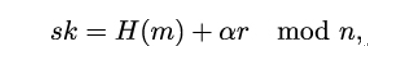
or equivalently,

Her signature is the pair sigAlice(m) = (r,s). She sends (m,sigAlice(m)) = (m,(r,s)) to Bob.

To verify Alice’s signature, Bob first obtains an authentic copy of Alice’s public key PKAlice = A. He then proceeds as follows:

1. He applies the hash function to m and gets the number H(m).
2. He computes the numbers u1 = s−1H(m) mod n and u2 = s−1r mod n.
3. He computes the point V = u1G + u2A = (xV ,yV ) on E. If xV mod n = r, the signature is verified.

Of course, for ECDSA the same cautionary remark applies as for DSA: the random integer k must be generated individually for each message m to be signed.

Example: Let Alice and Bob use the curve E : y2 = x3 + 7 over 𝔽37 and the public point G = (8,1) on E. Then the order of E is N = 39, and the order of the subgroup generated by G is n = 13. Figure 9.1 shows this curve, with the points of the subgroup generated by G highlighted.

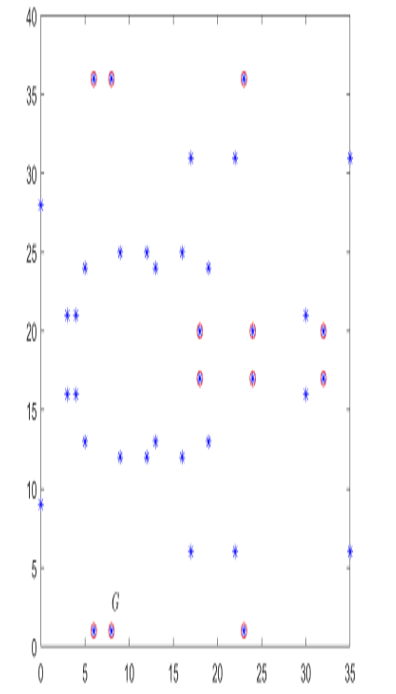
Figure 9.1: The curve E : y2 = x3+7 over 𝔽37. The points of the subgroup generated by G = (8,1) are drawn with an additional o symbol

In order to generate her key pair, Alice chooses α = 9 as her private key and computes the point A = αG = 9 ⋅ (8,1) = (23,1) as her public key.

Now, assume Alice wants to sign a message m with the hash value H(m) = 4. To do this, she chooses k = 7 and computes P = k ⋅ G = 7 ⋅ (8,1) = (18,20). Therefore, r = 18 mod 13 = 5. In order to compute s, we need the modular inverse of k = 7 modulo 13. Because 2 ⋅ 7 = 14 = 1 mod 13, we get k−1 = 2. Now

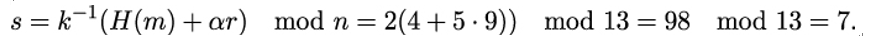
So, Alice sends

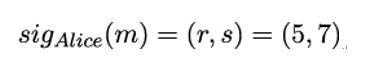
to Bob, along with m.

To verify Alice’s signature, Bob first obtains an authentic copy of Alice’s public key PKAlice = A = (23,1). He then computes the hash value over m. If m was not changed during transmission, he will get H(m) = 4. Next, Bob computes the numbers

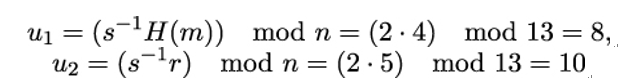
Now, he can compute the point V on E:

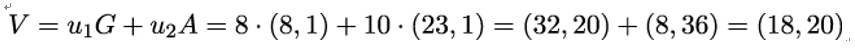
Finally, because xV mod n = 18 mod 13 = 5 = r, the signature is verified.