EdDSA algorithms 2 – Digital Signatures
The points on the elliptic curve form a group under addition, that is:
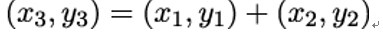
The neutral element for this group is (0,1). The explicit formulas for computing the points x3 and y3 are
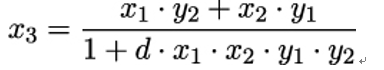
and
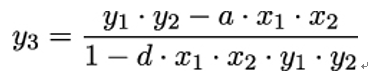
Unlike with many other elliptic curves, these formulas have the advantage of being complete. That means they are valid for all points on the elliptic curve, without exceptions. Specifically, the denominators in these formulas are non-zero for all input points.
Now, if Alice wants to generate an EdDSA signature for message M, she first needs a key pair consisting of a private EdDSA key and a public EdDSA key. To obtain the EdDSA private key, Alice simply generates a random b-bit string k.
To obtain the EdDSA public key, Alice first uses the cryptographic hash function h to compute H = h(k), the hash of her private key. She then computes:
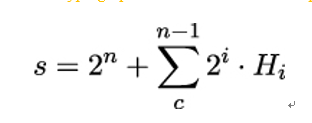
In binary representation, s is simply a bit string of length n where the n-th bit is set to 1, the bits from the n − 1-th to c-th bit are set to the corresponding bit values of Alice’s private key hash H, and the last 2 or 3 bits – depending on which value is chosen for c – are set to 0.
Using s, Alice computes the scalar multiple of B, the point on the elliptic curve we chose as the generator of the group (or subgroup) we want to work with:
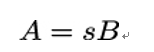
Finally, Alice computes ENC(A) where ENC is a specific encoding defined in RFC 8032. The resulting ENC(A) is Alice’s public EdDSA key.
To generate an EdDSA digital signature for message M under her private key k, Alice needs to compute the PureEdDSA signature of the prehashed message PH(M). Recall that PureEdDSA is simply an EdDSA where the prehash function PH is the identity function, that is, PH(M) = M.
To compute the PureEdDSA signature, Alice first computes two intermediate values R and S as follows:
- Compute the hash r = h(Hb∥…∥H2b−1∥M) using the bitwise concatenation of the previously computed hash H and Alice’s message M.
- Compute R as the scalar multiple R = rB.
- Using the previously computed value s, compute S as:
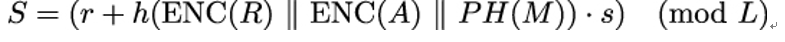
4. Output ENC(R) ∥ ENC(S) as the PureEdDSA signature of M.
To verify the PureEdDSA signature for Alice’s message M, Bob has to perform the following steps:
- Parse the PureEdDSA signature ENC(R) ∥ ENC(S) to obtain the values R and S.
- Compute H = h(ENC(R) ∥ ENC(A) ∥ M).
- Verify that:
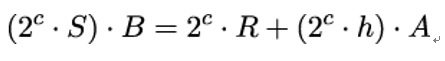
holds in E.
4. Reject the signature if parsing fails or the above equation does not hold. Otherwise, accept ENC(R) ∥ ENC(S) as a valid PureEdDSA signature of M.
EdDSA has several advantages compared to other digital signature schemes. First, it can be efficiently computed on various computer architectures and does not require a unique random number for each signature. This is especially advantageous for embedded systems where the available computing resources are always limited, and microcontrollers typically have no hardware-based random number generator.
Second, EdDSA uses small public keys and produces compact digital signatures. For the ed25519 algorithm, the public key is only 32 bytes and the digital signature is only 64 bytes. For the ed448 algorithm, the public key has 57 bytes and the digital signature has 114 bytes.
For comparison, the size of a signature generated with an RSASSA-PKCS1 v1.5 algorithm is l bytes, where l is the byte length of the RSA modulus n. Thus, if Alice uses RSA with, say, a 4,096-bit modulus, the size of the signature would be 512 bytes. And Alice should use RSA with a 4,096-bit modulus because achieving 128-bit security requires the modulus to be at least 3,200 bits, while the standard RSA settings used in practice are 1,024, 2,048, and 4,096 bits.
Third, the formulas used in EdDSA are complete in the sense that they are valid for all points on the curve. Consequently, there is no need to perform computationally expensive point validation for untrusted public values.
Finally, the PureEdDSA variant ensures collision resistance by construction. As a result, a potential collision of the hash function used in EdDSA does not break the signature scheme.
9.4.5 Legacy algorithms
The legacy algorithms define cryptographic algorithms as being deprecated because of known cryptographic weaknesses, specifically the SHA-1 hash function when used in either RSASSA-PKCS1 v1.5 or ECDSA.
The algorithms contained in this section of the TLS 1.3 SignatureScheme data structure concern only signatures appearing in digital certificates. In TLS 1.3, they are not allowed in CertificateVerify messages.