Digital signatures based on discrete logarithms – Digital Signatures
9.3 Digital signatures based on discrete logarithms
Other than for RSA signatures, we cannot create a signature based on discrete logarithms simply by encrypting the message m with a private key. This is because in the Diffie-Hellman protocol, we only agree on a shared secret between Alice and Bob. In the ElGamal scheme, Alice uses this shared secret, but not her private key for encryption. Moreover, Alice needs Bob’s public key to compute the shared secret. A digital signature scheme should work without knowing any other public keys than the signer’s, however.
The solution is to compute a number that depends on the private key α and to add this number to the hash value of the message to be signed. This number is masked with another secret parameter k so that the private key cannot be computed from the signature. The basic scheme can be found in the paper by ElGamal [62] from 1985. However, today, ElGamal signatures are not widely used because in 1990, Schnorr [160] found an improvement in the basic ElGamal scheme that is more efficient and uses shorter signatures. A closely related algorithm is known as the Digital Signature Algorithm (DSA) and was adopted in 1991 by the National Institute of Standards and Technology (NIST) as the Digital Signature Standard (DSS) for the United States.
Note that in the latest version of the DSS [135], the DSA over a finite field is no longer approved for signature generation, and only the Elliptic Curve DSA (ECDSA) shall be used. Nevertheless, we discuss the DSA over finite fields in the next subsection because it still needs to be implemented in order to verify earlier signatures generated by DSA. Moreover, we think that the ECDSA is easier to understand if the DSA is discussed first.
9.3.1 Digital Signature Algorithm (DSA)
To set up the scheme, Alice and Bob agree on the following parameters [102]:
- A prime q of N bits, where N must not be larger than the bitlength of the hash function H (see Chapter 11, Hash Functions and Message Authentication Codes) used for signing.
- A second, larger prime p so that q is a large divisor of p − 1.
- A generator g of the cyclic subgroup of 𝔽p∗ of order q. In order to do so, Alice and Bob choose a random g0 ∈𝔽p∗ and check if
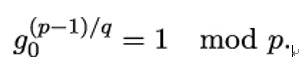
If this is not the case, g = g0(p−1)∕q mod p is a generator.