IT Certification Exams and Digital Signatures

Digital signatures based on discrete logarithms 2 – Digital Signatures

• Ella Andrus
• 2022-10-202024-08-31
• 0

To generate her signing key, Alice performs the following steps:

1. She takes a random α, where 0 < α < q as her secret signing key SKAlice.
2. Her public key is PKAlice = A = gα mod p.

To sign a message m, Alice takes the following steps:

1. She applies a hash function H to m. The result H(m) should be in the range 0 < H(m) < q.
2. She picks a random integer k, where 0 < k < q, computes gk mod p, and sets

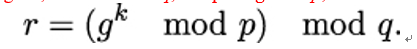
3. Finally, Alice finds an integer s such that

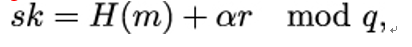
or equivalently,

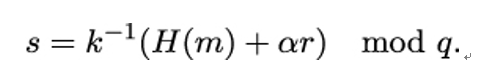
Her signature is the pair sigAlice(m) = (r,s). She sends (m,sigAlice(m)) = (m,(r,s)) to Bob.

To verify Alice’s signature, Bob first obtains an authentic copy of Alice’s public key PKAlice = A. He then proceeds as follows:

1. He applies the hash function to m and gets the number H(m).
2. He then computes u1 = s−1H(m) mod q and u2 = s−1r mod q.
3. He then computes gu1Au2 mod p. If the result agrees with r modulo q, the signature is verified.

The scheme works because

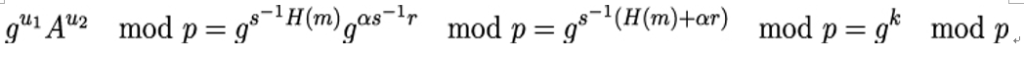
Moreover,

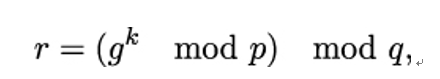
because this was how Alice had defined the number r when she signed m.

It is important that the integer k in the signing step is chosen individually for each message m to be signed. Otherwise, if k is the same for two messages m1,m2, the first part r of the signature is the same. Moreover, we have

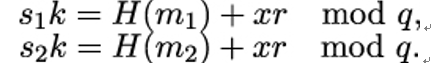
Eve can solve this system of equations for k:

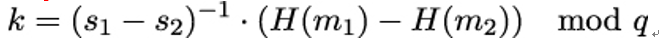
Now Eve can forge Alice’s signature over some message mEve.

Indeed, sigAlice(mEve) = (r,sEve), where

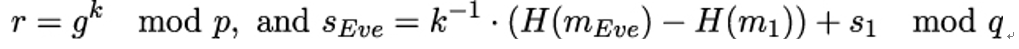
Example: To set up the scheme, Alice and Bob agree on the prime numbers q = 11 and p = 23. Then 2p−1∕q = 22 = 4≠1 mod 23, so they can use g = 4 as the generator.

Now, Alice chooses α = 3 as her signing key SKAlice. Consequently, her public key is PKAlice = A = 43 mod 23 = 18. In order to sign her message m, she applies the hash function on it and gets H(m) = 5 as the result. She now picks k = 7 randomly and computes the number

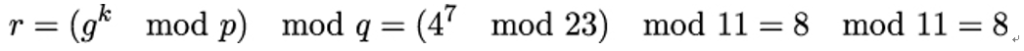
Now, she needs to find 7−1 mod 11. Because 7 ⋅ 8 = 56 = 1 mod 11, she gets 7−1 = 8 and can compute the second part of the signature:

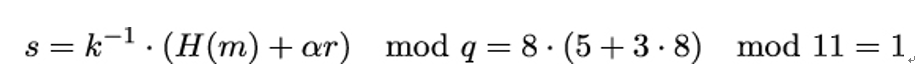
Alice sends (m,(r = 8,s = 1)) to Bob.

In order to verify the signature, Bob hashes m and gets H(m) = 5, if the message was not modified during transit. He also needs to compute s−1 mod q. But s = 1, so s−1 = 1 as well. He can now compute u1 = s−1H(m) mod q = 5 mod 11 = 5 and u2 = s−1r mod q = 8 mod 11 = 8.

Bob now computes

This number needs to agree with r = 8 (modulo q). But q = 11, so Bob gets 8 mod 11 = 8 = r, and the signature is verified.