Curve secp521r1 – Elliptic Curves
8.5.3 Curve secp521r1
The third NIST curve included in the TLS 1.3 standard is curve secp521r1. It is also defined in FIPS-186 where it is referred to as curve P-521. P-521 is defined over the prime field 𝔽p with p = 2521 − 1.
Like P-256 and P-384, the curve P-521 is defined by the equation:
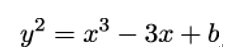
with the SHA-1 seed value for coefficient b being:
d09e8800 291cb853 96cc6717 393284aa a0da64ba
The security strength of curve P-521 is 256 bits. As with all elliptic curves, this only holds as long as Eve uses classical computers. If a large enough quantum computer is ever built and Eve can use it to attack the elliptic curve-based key establishment phase between Alice and Bob, she will be able to determine their secret key in polynomial time.
From the security perspective, there is a potential downside all three NIST curves – P-256, P-384, and P-521 – have in common. Specifically, it has to do with these curves being pseudo-random.
Previously in this chapter, we saw that the security of elliptic curve cryptography – for instance, the security of the key establishment between Alice and Bob when they use the ECDH protocol – depends on the computational hardness of ECDLP.
We also discussed that not all elliptic curves are suitable for cryptography as there are curves for which ECDLP can be solved in practice even using today’s classical computers. As a result, such curves are not suitable for cryptographic applications.
When parameters defining an elliptic curve, for instance, its coefficients, are given without a concise explanation of how one has arrived at these specific values, there is a risk of a cryptanalytic backdoor. Specifically, Eve might have found a new attack known only to her and propose to standardize one or more curves that are vulnerable to this attack [22].
NIST curves P-256, P-384, and P-521 are generated using SHA-1 seeds that cannot be explained. As a result, some cryptographers voiced concerns that these curves might be deliberately chosen to have a mathematical weakness only known to the National Security Agency (NSA), which helped NIST to specify them.
NIST has claimed that the use of SHA-1 to compute coefficient b ensures the curves were not predetermined because of the following:
- It can be verified that b is derived from the specific seed
- Given the properties of cryptographic hash functions, it is computationally infeasible to find an input seed that yields the desired hash value
However, Bernstein and Lange pointed out [22] that having enough computing resources, an attacker could simply generate curves for a large number of random parameters until they find a weak curve.