Curve secp256r1 – Elliptic Curves
8.5.1 Curve secp256r1
Digital Signature Standard FIPS-186 [128] specifies 15 elliptic curves that the National Institute of Standards and Technology (NIST) recommends for use by the US federal government. All 15 curves were generated using a method described in the IEEE 1363-2000 and the ANS X9.62 standards.
Curve secp256r1 is one of the elliptic curves defined in FIPS-186. In the standard, it is referred to as curve P-256. The curve is defined over a prime field 𝔽p with the prime p = 2256 − 2224 + 2192 + 296 − 1, hence the name P-256.
Curve P-256 is defined by the equation:
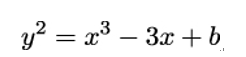
The coefficient −3 (mod p) in the term −3x was chosen for reasons of computational efficiency. The coefficient b is generated based on the output of a cryptographic hash function, making P-256 a pseudo-random curve. In FIPS-186, the hash function used is the – in the meantime outdated and insecure – SHA-1 algorithm.
More precisely, coefficient b is computed in two steps:
- Taking a 160-bit input seed specified for curve P-256 and computing SHA-1 output c for this seed value.
- Then computing b such that b2c = −27 (mod p).
As an example, the SHA-1 input seed for curve P-256 in hexadecimal notation is:
c49d3608 86e70493 6a6678e1 139d26b7 819f7e90
P-256’s security strength is equivalent to that of a 128-bit block cipher. In other words, with the currently known cryptanalytic techniques, Eve would need to perform 2127 guesses on average to break a cryptosystem whose security is based on curve P-256. However, this only applies as long as Eve has no access to a large enough quantum computer.
8.5.2 Curve secp384r1
Curve secp384r1 is another elliptic curve over the prime field defined in FIPS-186 where it is referred to as curve P-384. It is defined over the prime field 𝔽p with p = 2384 − 2128 − 296 + 232 − 1.
Like P-256, the elliptic curve P-256 has the form:
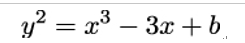
with the SHA-1 seed value for generating coefficient b defined as:
a335926a a319a27a 1d00896a 6773a482 7acdac73
Curve P-384 has the security strength of 192 bits against attacks using classical computers.