Curve 25519 – Elliptic Curves
8.5.4 Curve 25519
Curve 25519 is defined in RFC 7748, where it is referred to as curve25519. It was proposed in 2005 by the American-German cryptographer Dan Bernstein [24] and attracted interest from the wider cryptographic community after the discovery of a potential backdoor in the Dual Elliptic Curve Deterministic Random Bit Generator (Dual_EC_DRBG) algorithm based on the then-popular standardized elliptic curve P-256.
curve25519 is an elliptic curve over a prime field 𝔽p where p is equal to 2255 − 19, hence the name of the curve. It is a so-called Montgomery curve defined by the equation:
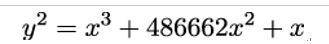
Montgomery curves are simply a special form of elliptic curves defined by equations of the form By2 = x3 + Ax2 + x where B≠0 and A≠ ± 2.
curve25519 offers a security level of approximately 128 bits. In other words, the curve25519 security level is roughly equivalent to that of a 128-bit block cipher. Importantly, curve25519 is generated in a deterministic way to meet a number of required (security) properties. Why is this important? As discussed earlier in this chapter, if the generation process of a specific elliptic curve can be fully explained, Alice and Bob are assured that the curve was not generated to be weak.
Otherwise, Eve could join a standardization effort and propose standardizing an elliptic curve vulnerable to some secret attack that only Eve knows about. As a result, as long as that attack remains unknown to the public, Eve would be able to completely break the security of the communication channel between Alice and Bob completely unnoticed, that is, without having to tamper with the communication traffic.
curve25519 properties allow you to implement constant-time computation and a scalar multiplication that, by design, will never produce exceptions. The constant execution time is ensured by the design of curve25519 where the same sequence of computations is done for all secret key values.
As a result, Alice and Bob can use X25519 (the key agreement scheme based on curve25519) implementations that are resistant to various types of so-called side channel analysis, an implementation-level attack exploiting the statistical link between the intermediate values processed by a cryptographic algorithm and physical quantities such as instantaneous power consumption, execution time, or cache-based timing patterns, just to name a few.
In addition, cryptographic computations based on curve25519 are fast on a wide range of instruction set architectures. Thanks to careful design choices, cryptographic operations on curve25519 can be performed about twice as fast compared to other elliptic curves with a similar security level.