IT Certification Exams and Digital Signatures

Algorithms for solving special cases of ECDLP – Elliptic Curves

• Ella Andrus
• 2024-08-312024-08-31
• 0

8.4.2 Algorithms for solving special cases of ECDLP

Because of their mathematical properties, some elliptic curves allow you to take shortcuts when solving ECDLP. In 1991, mathematicians Alfred Menezes, Scott Vanstone, and Tatsuaki Okamoto published an algorithm that reduces ECDLP to a DLP in the multiplicative group of a finite field.

They showed that for supersingular elliptic curves, the reduction takes probabilistic polynomial time. This, in turn, can undermine the security of an elliptic curve because subexponential algorithms are known for solving DLP in finite fields.

The Menezes-Vanstone-Okamoto (MOV) algorithm uses a so-called bilinear map e to map two points on an elliptic curve E defined over a field 𝔽q to an element in the finite field 𝔽qd where d is the embedding degree specific to the elliptic curve E.

Let G be a base point on an elliptic curve E and 𝔾 be a cyclic group of order n generated by G. Further, let Q be another point on curve E that has order n and is linearly independent to G, in other words, there is no such m that Q = mG.

Finally, let P = kG with some unknown, unique integer k that we must find to solve ECDLP. The MOV algorithm solves ECDLP as follows:

1. Compute the bilinear maps e(G, Q) and e(kG, Q).
2. Observe that – because e is bilinear – the following equation holds:

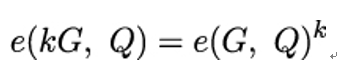
3. Based on the observation in step 2, set u = e(G, Q) and v = e(kG, Q). It holds that:

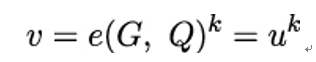
4. Solve the DLP in the finite field 𝔽qd by finding the unique integer k given uk and u.

As a result, the MOV algorithm reduces solving ECDLP on the elliptic curve E to solving DLP in the finite field 𝔽qd. Whether this has an impact on the security of an elliptic curve or not depends on the specific choice of the curve.

For most randomly chosen elliptic curves, the MOV algorithm reduces ECDLP on these curves to a much harder DLP in the corresponding finite field [166] because the embedding degree d is very large.

However, some curves can be mapped to finite fields with a small embedding degree where solving DLP is computationally feasible. As an example, let E be a supersingular elliptic curve defined over the finite field 𝔽p where p ≥ 5 is a prime.

Now suppose we choose as the base point a point G of order n that divides the total number of points on E. In that case – we omit the exact mathematical explanation here – n has an embedding degree 2 in 𝔽p. As a result, ECDLP on a supersingular elliptic curve over 𝔽p can be reduced to solving DLP in 𝔽p2 for which subexponential algorithms are known [166]. This is also the reason why, in general, supersingular curves are not be used in elliptic curve cryptography.

Another special case are so-called anomalous elliptic curves. An anomalous elliptic curve E is a curve defined over a finite field 𝔽p where p ≥ 3 and the number of points in E is equal to p. For such curves, the following algorithm can be used to solve ECDLP:

1. Let P,G be points in anomalous elliptic curve E defined over a finite field 𝔽p, and P = kG with the unknown unique integer k.
2. Choose a second elliptic curve E′ defined over the field of p-adic numbers ℚp whose reduction modulo p is the original curve E.
3. Lift points P,G to points P′,G′ in E′ (again, we omit the mathematical details of how this is done or why it works).
4. Compute pa = log E(pP′) and pb = log E(pG′).
5. Finally, compute k = a−1b (mod p).

Because of these efficient algorithms to solve the ECDLP, anomalous and supersingular elliptic curves are mostly ruled out for cryptographic purposes. So, which properties does a secure elliptic curve need to have?